タグ

固体電解質バンドギャップ Quantum ESPRESSO LLZO H200 NVL GPU シミュレーション GPU dos

H200 NVLで可視化：Li（金属）と LLZO（固体電解質）のDOS比較

Quantum ESPRESSO 7.4.1 / PBE / Li-bcc と LLZO の DOS（状態密度）を GPUで短時間に可視化

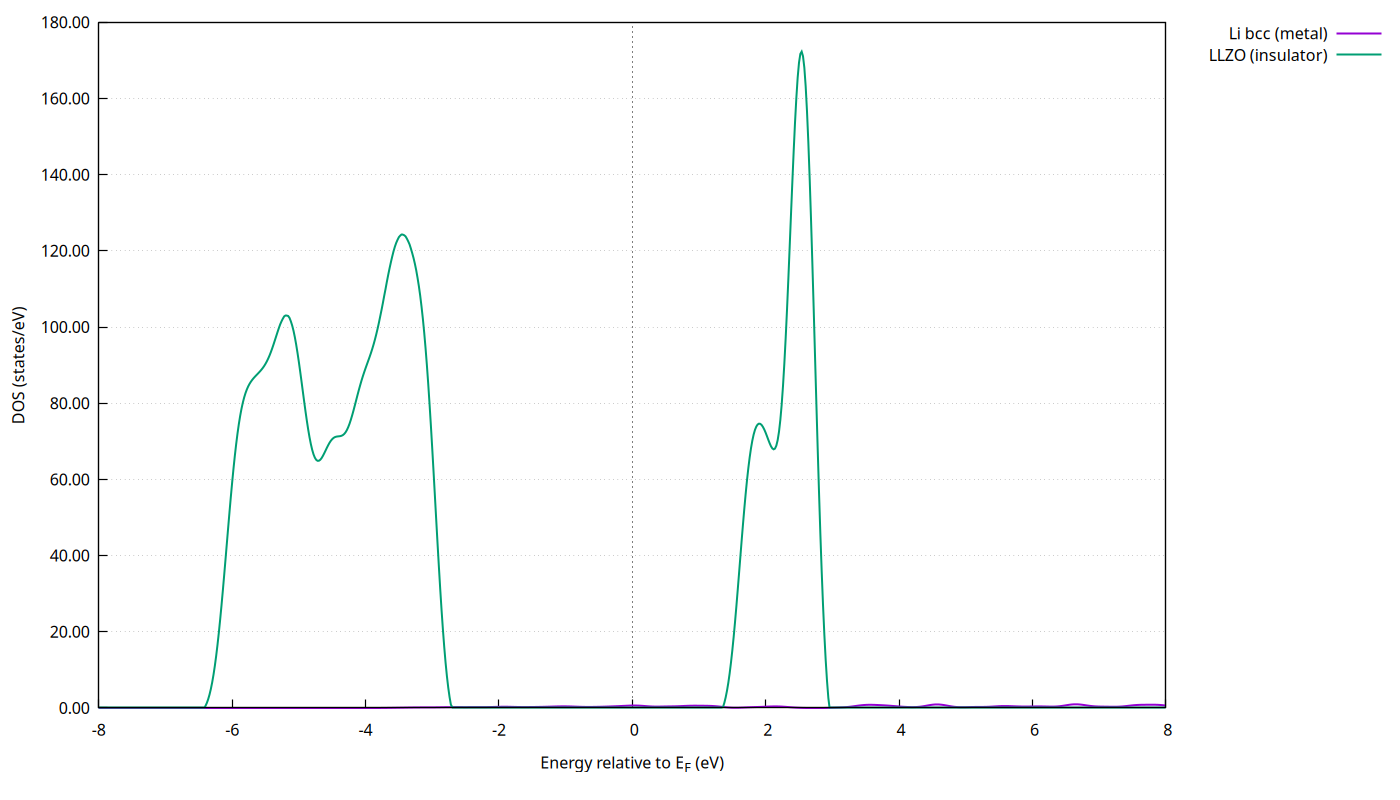
Li（金属）はフェルミ準位 E_F で DOS > 0（電子が動ける）、LLZO は E_F 近傍で DOS ≈ 0（バンドギャップあり）。シンプルな可視化でも「電子を通す材料／遮る材料」の違いが一目で分かります。この記事は H200 NVL 4/8 GPU サーバーでの再現を前提に、入力と実行コマンドを公開します。単体の計算としては軽量ですが、実際の研究ではセルサイズや k 点密度、ドーピング条件や界面構造を変えたケースを数十〜数百本まとめて回すため、H200 NVL 4/8 GPU のスループットが効いてきます。

H200 NVL 4GPU の構成・価格を見る H200 NVL 8GPU の構成・価格を見る

TL;DR（先に結論）

材料	特徴	可視化からの示唆
Li（bcc, 金属）	E_F で DOS > 0	バルクは電子伝導性が高い
LLZO（固体電解質）	E_F 近傍で DOS ≈ 0、しきい値法でギャップ ≈ 2.68 eV	電子は通しにくい（イオン選択性の一端）

※ 本記事のギャップ値は DOS カーブからの近似です。厳密なバンドギャップはバンド構造や k 点密度、手法に依存して変わります。

図：E_F を揃えた Li と LLZO の DOS

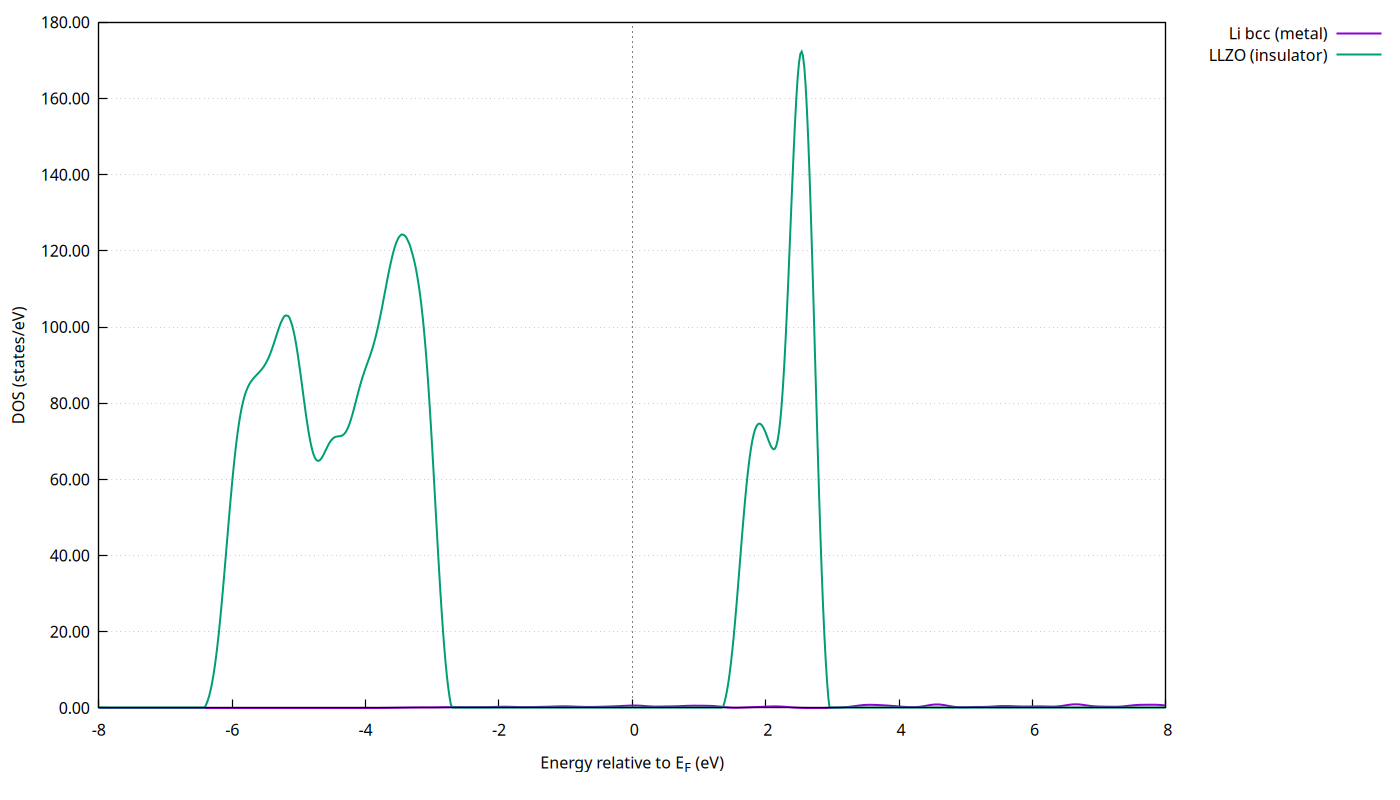
Li（金属）と LLZO（固体電解質）の DOS 比較（E−EF基準）。Li は E_F で DOS>0、LLZO はギャップで DOS≈0。 — 横軸：E 相対値（E − E_F）、縦軸：DOS（states/eV）。Li は金属、LLZO は絶縁性を示す。

※ 画像は記事内スクリプトで生成したものです。CMSのメディアにアップ後、上の src をメディアURLへ差し替えてください。

なぜ DOS を見るのか（超要点）

DOS（状態密度）は「あるエネルギーに電子が占められる状態がどれくらい存在するか」を表します。
金属： フェルミ準位 E_F で DOS > 0 → 電子がすぐ励起・伝導できる。
絶縁体： E_F 前後で DOS ≈ 0 → バンドギャップがあり、電子が動きにくい。

固体電池では「イオンは通すが電子は通しにくい」材料が望ましく、LLZO のような固体電解質はその要件に合う候補です（実際の挙動は欠陥・界面・不純物・電位など多要因で決まります）。

Li/LLZO 界面では、界面欠陥や電位分布の乱れによって局所的に電子が漏れ、それが Li デンドライト萌芽のきっかけになると考えられています。本記事の単純な DOS 比較は、「バルクとして LLZO は電子を通しにくい」という直感を整理する入り口であり、界面や欠陥を含むより重いシミュレーション（今後の LLZO–Li 連載）につなぐ位置づけです。

結果サマリ（今回のログに基づく概算）

Li bcc（12×12×12 k点, PBE）SCF時間：数秒（1セル）
LLZO DOS 後処理：数十秒（保存済み .save から dos.x 実行）
しきい値法（|DOS| > 1e-3 states/eV）で LLZO のギャップ推定：≈ 2.68 eV
GPU 化された pw.x / dos.x を用いることで、同じ規模の計算でも CPU のみの環境に比べて壁時計時間を大きく短縮できるケースが多く、パラメータスタディの回転数を上げやすくなります。

注：時間は今回の実行例に基づく概算です。セルサイズ、k点、擬ポテンシャル、GPU/CPU構成、UCX/MPI設定で変動します。

再現手順（コピー＆ペーストOK / 最小セット）

1) 環境（PATH と MPI/UCX を最小設定）

# ~/qe_env_min.sh
export PATH=$HOME/src/q-e-qe-7.4.1/bin:$HOME/bin:$PATH
export OMPI_MCA_coll_hcoll_enable=0
export OMPI_MCA_pml=ucx
export OMPI_MCA_btl=^openib
export UCX_TLS=sm,self,cuda_copy,cuda_ipc
# 実行前に読み込み
source ~/qe_env_min.sh

2) Li（bcc）のSCF

li_bcc_scf.in を保存し、pseudo/ に Li の擬ポテンシャル（例：Li.pbe-s-van_ak.UPF）を置きます。

&control
  calculation = 'scf'
  prefix      = 'li_bcc'
  outdir      = './tmp/li_bcc'
  verbosity   = 'low'
/
&system
  ibrav = 3,  A = 6.345
  nat = 1, ntyp = 1
  ecutwfc = 50, ecutrho = 400
  occupations = 'smearing', smearing = 'mp', degauss = 0.02
/
&electrons
  conv_thr = 1.0d-10
/
ATOMIC_SPECIES
  Li  6.941  Li.pbe-s-van_ak.UPF
ATOMIC_POSITIONS crystal
  Li  0.0  0.0  0.0
K_POINTS automatic
  12 12 12  0 0 0

# 実行（4ランク例）
mpirun -np 4 pw.x -in li_bcc_scf.in | tee li_bcc_scf.out

3) Li の DOS（省メモリ：1ランク）

&dos
  outdir = './tmp/li_bcc'
  prefix = 'li_bcc'
  fildos = 'li_bcc.dos'
  Emin   = -50.0, Emax =  50.0, DeltaE = 0.01
  ngauss = 1, degauss = 0.02
/

mpirun -np 1 dos.x -in li_bcc_dos.in | tee li_bcc_dos.out

4) LLZO の DOS（保存済み `.save` を自動検出して実行）

# ./tmp/*/*.save のうち "llzo" を含む最新のものを使う
cand=$(ls -dt ./tmp/*/*.save 2>/dev/null | grep -i '/llzo' | head -n1)
odir=$(dirname "$cand"); pref=$(basename "$cand" .save)

cat > llzo_dos.in << EOF
&dos
  outdir = '$odir'
  prefix = '$pref'
  fildos = 'llzo.dos'
  Emin   = -50.0, Emax =  50.0, DeltaE = 0.01
  ngauss = 1, degauss = 0.02
/
EOF

mpirun -np 1 dos.x -in llzo_dos.in | tee llzo_dos.out

5) E_F 揃え（相対エネルギーに平行移動）

# Fermi を取得
liEF=$(awk '/EFermi/{print $(NF-1)}' li_bcc.dos)
llzoEF=$(awk '/EFermi/{print $(NF-1)}' llzo.dos)

# E を (E - EF) に変換。1列目: 相対E [eV], 2列目: DOS
awk -v EF="$liEF"  'NR>1{printf "%10.4f %14.6e\n",$1-EF,$2}'  li_bcc.dos > li_bcc.dos.rel
awk -v EF="$llzoEF" 'NR>1{printf "%10.4f %14.6e\n",$1-EF,$2}' llzo.dos   > llzo.dos.rel

6) しきい値法で LLZO のギャップを概算

T=1e-3 # states/eV
Evbm=$(awk -v T=$T '$1<0 && ( ($2>0?$2:-$2) > T ){ev=$1} END{print (ev=="" ? "NaN": ev)}' llzo.dos.rel)
Ecbm=$(awk -v T=$T '$1>0 && ( ($2>0?$2:-$2) > T ){print $1; exit}' llzo.dos.rel)
awk -v Ev="$Evbm" -v Ec="$Ecbm" 'BEGIN{Eg=Ec-Ev; printf("LLZO gap (DOS法): Eg ≈ %.3f eV\n",Eg)}'

7) 参考：gnuplot で図を再現

gnuplot -persist << 'GP'
set term pngcairo size 1280,720
set output 'dos_li_vs_llzo_EminusEF.png'
set grid
set xlabel "Energy relative to E_F (eV)"
set ylabel "DOS (states/eV)"
set arrow from 0,graph 0 to 0,graph 1 nohead dt 3 lw 1
plot [-8:8] 'li_bcc.dos.rel' u 1:2 w l title 'Li bcc (metal)', \
             'llzo.dos.rel'  u 1:2 w l title 'LLZO (insulator)'
GP

擬ポテンシャル例：Li.pbe-s-van_ak.UPF、La/Zr/O は PSLibrary 系（例）。ご利用のライセンス/出典表記に従ってください。

サンプル入力・スクリプト一式（GitHub）

本記事で使用している Quantum ESPRESSO の入力ファイルや gnuplot スクリプト一式は、GitHub リポジトリにまとめておくと、読者がそのままダウンロードして H200 NVL サーバー上で再現しやすくなります。

サンプル入力を GitHub から取得する

※ 擬ポテンシャルファイルはライセンスの関係で同梱せず、入手元へのリンクとファイル名のみを記載する運用がおすすめです。

H200 NVL サーバーで進める理由（営業的な要点だけ）

大セル・高密 k点の反復を短縮：GPU 対応版 pw.x がハミルトニアン適用などのボトルネックを高速化し、LLZO のような大きな単位格子でも実用時間内に収束させやすくなります。
NVLink/NVL による高速 GPU 間通信：H200 NVL 4/8GPU 構成では、1 ノード内での GPU 間データ転送が高速で、バンド並列・k 点並列の効率が出しやすくなります。
研究の回転数アップ：構造最適化 → SCF → DOS/PDOS → 可視化 → 条件見直し、というループの壁時計時間を短縮し、Li/LLZO 界面や欠陥・ドープ系の多数ケースを短期間でスクリーニングできます。
より重い計算へのスケールアップが容易：本記事のような単純な DOS 可視化から、界面モデル・AIMD・ML-IAP を組み合わせた大規模計算まで、同じ H200 NVL プラットフォーム上で拡張していけます。

※ 実効性能は入力規模・擬ポテンシャル・ソルバー・MPI/UCX 設定・CPU 性能などで変わります。評価用にチューニングした入力一式は個別にご提供可能です。

お問い合わせ・お見積りはこちら

電子はどこを通る？Li vs LLZOをDOSで一目比較（GPU実測ログ付き）